1 A classroom that normally contains 40 people
is to be air conditioned with window air conditioning units of 6 kW cooling
capacity. A person at rest may be
assumed to dissipate heat at a rate of about 360 kJ/h. There are 10 light bulbs in the room, each
with a rating of 100 W. The rate of heat
transfer to the classroom through the walls is 15,000 kJ/h. If the room air is to be maintained at a
constant temperature of 21oC, determine the number of
air-conditioning units required.
In this problem, we define
the system to be the air in the room. We
can assume that the air behaves as an ideal gas. If the temperature remains constant, there is
no change in the internal energy of the air.
Since the volume of the room remains constant, there is no work done.[1] Thus the first law reduces to the equation
that Q = 0. We account for the different
heat sources in the total heat rate, Q, as follows. The heat input comes (a) from the 40
students, Qs = (40 people)(360 kJ/h•person)(kW•s /kJ)(h/3600 s) = 4
kW, (b) heat transfer through the wall, Qw = (15,000
kJ/h)(kW/kJ•s)(h/3600 s) =4.167 kW, and (c) heat added by the light bulbs, Qb
= 10(100 W) = 1000 W = 1 kW. Thus the
total heat input is 4 + 4.167 + 1 = 9.167 kW.
The heat removal comes from the air conditioners which remove 5 kW
each. Thus for the net Q to be zero we
must have N air conditioners such that (5 kW)N = 9.167 kW. To satisfy this requirement, we must have two air conditioning
units.
2 A 0.5 m3 rigid tank contains
regrigerant-134a initially at 160 kPa and 40% quality. Heat is now transferred to the refrigerant
until the pressure reaches 700 kPa.
Determine (a) the mass of refrigerant in the tank and (b) the amount of
heat transferred. Also, show the process
on a P-v diagram with respect to the saturation lines.
The mass of refrigerant
may be found from the initial state using the equation that m = V / v1
where V = 0.5 m3 and v is found from the temperature and the
quality. Since we are given an initial
quality, x1 = 40%, we know that we are in the mixed region. The specific volume is found from the
specific volumes of the saturated liquid and vapor, which are found in Table
A-12 on page 930: vf(160 kPa) = 0.0007437 m3/kg and vg(160
kPa) = 0.12348 m3/kg. We then
find the initial specific volume as follows.
With this specific volume,
we then find the refrigerant mass as follows:
[1] Note that is both the mass and volume remain
constant, the specific volume remains constant.
Since both the temperature and specific volume are constant, the
internal energy is a constant, regardless of whether or not we assume that air
is an ideal gas.
To compute the heat
transfer we apply the first law, Q = DU + W. We assume that there is no
volume change in the “rigid” tank. If
there is no volume change, no work is done.
With W = 0, Q = DU. We find DU = m(u2 – u1) where the specific internal energies
are found from the property tables. At
the initial state we find u from the quality in the same way that we found the
volume.
Because this is a constant volume process, the
final state has the same specific volume as the initial state (0.049838 m3/kg)
and a given pressure of 700 kPa. Knowing
these data we can plot the constant volume path for this process as shown in
the figure at the left. We see that the
initial state (1) is in the mixed region and the increase in pressure, at
constant volume, brings the final state into the gas region. Plot for problem 2
When we try to find the
final state (P = 700 kPa, v = 0.049838 m3/kg) in the superheat table,
A-13, on page 930, we see that the final specific volume in the table for P =
700 kPa = 0.70 MPa (at a temperature of 160oC) is only 0.048597 m3/kg. Furthermore, the specific volume is
increasing with temperature so that the final state is at a higher temperature
than the final temperature in the table.
The internal energy at the
final state can be found by extrapolation beyond the last value in the table,
using the same formula as for interpolation, with the last two points in the
table.
We can now find the heat
transfer as follows.
3 A 20 ft3 rigid tank contains
saturated regrigerant-134a vapor at 160 psia.
As a result of heat transfer from the refrigerant, the pressure drops to
50 psia. Show the process on a P-v
diagram with respect to the saturation lines, and determine (a) the final
temperature, (b) the amount of refrigerant that has condensed, and (c) the heat
transfer.
The solution of this
problem is similar to the previous one.
It is a constant volume process so that the work is zero and the heat
transfer equals the change in internal energy.
The P-v diagram for this problem is shown below. The process starts at the saturated vapor
line at 120 psia and as heat is removed, some refrigerant condenses, moving the
process into the mixed region at the final state where P2 = 50 psia..
Since the final state is
in the mixed region, we know that the final temperature is the saturation
temperature at the final pressure of 50 psia.
From table A-12E on page 977, we find that the final temperature, Tsat(50
psia) = 40.23oF.
|
The amount of refrigerant that has condensed
is the total mass minus the mass that is vapor at the final state. This is m – x2m. We can find the total mass from the specific
volume at the initial state and the total volume of the container: m = V/v1,
where v1 is the volume of the saturated vapor, vg, at the
initial pressure of 160 psia. From Table
A-12E on page 977 we find that vg(160 psia) = 0.29316 ft3/lbm,
so that the total mass is given by the following equation.
Problem 3
The specific volume at the
final state is the same as the initial specific volume, so we can find the
quality at this final state from the saturated liquid and vapor specific
volumes at the final pressure of 50 psia, taken from Table A-12E.
The mass condensed can now
be found.
mcondensed = m
– mx2 = (1 – x2) m = ( 1 – 0.3000 ) ( 68.222 lbm
) = 47.75
lbm.
We have to find the
internal energy at the initial and final states to compute the heat
transfer. The initial internal energy is
simply ug(160 psia) = 108.50 Btu/lbm (Table A-12E). The internal energy at the final state is
found from the saturation properties and the quality, x2 = 0.3000.
The heat transfer can now
be found from the first law.
Q = DU + W = m(u2 –
u1) + W = (68.222 lbm)(47.396 – 108.50) Btu/lbm
+ 0 = –4 ,169
Btu.
4 An insulated piston-cylinder device contains
5 L of saturated liquid water at a constant pressure of 175 kPa. Water is stirred by a paddle wheel while a
current of 8 A flows for 45 min through a resistor placed in the water. If one half of the liquid is evaporated
during this constant-pressure process and the paddle-wheel work amounts to 400
kJ, determine the voltage of the source.
Also, show the process on a P-v diagram with respect to the saturation
lines.
In this problem we assume
that the insulation on the piston-cylinder device reduces the heat transfer to
a negligible amount so that we may assume that Q = 0. The evaporation of the liquid comes from the
addition of work from the resistor and the paddle wheel. At the same time, the piston is expanding, at
constant pressure, so that the water is doing work. Since the pressure is constant, this work is
simply equal to P(V2 – V1).
For this problem the first
law becomes:
Q = 0 = DU + W = m(u2 –
u1) + P(V2 – V1) + Wresistor + Wpaddle
We can write the volumes
as the product of mass times specific volume and use the fact that P = P1
= P2 to introduce the enthalpy, h = u + Pv.
–Wresistor – Wpaddle
= m(u2 – u1) + Pm(v2 – v1) =m[(u2
+ P2v2) – (u1 + P1v1)] =
m(h2 – h1)
We can find the mass from
the initial state where we know V1 = 5 L and v1 = vf(P1
= 175 kPa). Using Table A-5 on page 916
to find vf, we compute the mass as follows.
Since the paddle wheel and
resistance work are inputs, these are negative.
Thus the values of Wresistor and Wpaddle are –EIDt and –400 kJ, where E is
the voltage that we want to find and I is the given current of 8 A. The enthalpy at the initial state is simply hf
at 175 kPa. The enthalpy at the final
state is the enthalpy of a mixture with a quality of 50% at the same 175 kPa
pressure. We thus have h1 = hf(175
kPa) = 487.01 kJ/kg, where we use Table A-5 for the saturation data. Using the same table and the value of x2
= 50% we find h2 as follows.
Substituting the work
terms and enthalpy and mass into our first law gives an equation for the
unknown voltage.
–Wresistor – Wpaddle
= EIDt + 400 kJ = m(h2
– h1) = (4.730 kg)(1593.56 – 487.01) kJ/kg
Combining the numerical data gives an
equation for the work done by the resistor.
EIDt
= 4834 kJ = 4834 kW•s
We can solve this to find the voltage
applied to the resistor.
5 A piston-cylinder device initially contains
steam at 200 kPa, 200oC, and 0.5 m3. At this state a linear spring (F a x) is
touching the piston but exerts no force on it.
Heat is now slowly transferred to the steam causing the pressure and the
volume to rise to 500 kPa and 0.6 m3, respectively. Show the process on a P-v diagram with
respect to the saturation lines and determine (a) the final temperature, (b)
the work done by the steam, and (c) the total heat transferred.
The path for this process is shown in the diagram below. The initial point of the path is (P1, V1) = (200 kPa, 0.5 m3); the final point is (P2, V2) = (500 kPa, 0.6 m3).
The total pressure, P,
acting on the water will be the sum of the constant pressure from the weight of
the piston (and atmospheric pressure), P1, and Pspring.
This equation is seen to provide a
linear relationship between pressure and volume as shown in the diagram
above. The work is the area under the
path which is the area of a trapezoid: W = (P1 + P2)(V2
– V1)/2. Using the values of
pressure and volume given in the problem allows us to find the work.
The heat transfer is given
by the first law: Q = DU + W
= m(u2 – u1) + W.
We have to find the values of u1 and u2 from the
property tables for water. In addition,
we can find the mass from the initial volume, V1 = 0.5 m3,
and the initial specific volume, v1.
At the initial state of P1
= 200 kPa and T1 = 200oC, we find the following
properties in the superheat table, Table A-6 on page 918: v1 = 1.08049
m3/kg and u1 = 2654.6 kJ/kg. We can then find the mass as follows.
From this system mass, we
can compute the specific volume at the final state where V2 = 0.6 m3.
At the final pressure of
500 kPa, the specific volume, v2 = 1.2966 m3/kg occurs
between temperatures of 1100oC and 1200oC in Table A-6 on
page 920. Interpolating between these
two points gives the temperature and internal energy at the final state.
`
So, the final temperature,
T2 = 1132oC.
The heat transfer is found
from the first law as usual.
Q = m(u2 – u1)
+ W = (0.46275 kg)(4325.8 – 2654.6)kJ/kg + 35 kJ = 808 kJ.
The P-v diagram for this
process is shown at the right. During the
first part of the process, from point 1 to point 2, the pressure is too low to
lift the piston, so the process occurs at constant volume. Once the pressure reaches 300 kPa, the
piston starts to rise and the remainder of the expansion (a doubling of volume)
occurs at constant pressure.
The total heat transfer is
found from the first law as Q = DU + W = m(u3 – u1) + W, where W is found as the
area under the path: W = P2-3(V3 – V1) and P2-3
is the constant pressure of 300 kPa = P2 = P3. We know that V1 = 0.8 m3
and V3 = 2 V1 = 1.6 m3. Thus, the work is found as follows.
The mass is found from the
initial volume of 0.8 m3 and the initial specific volume which is
the specific volume of a saturated vapor at 250 kPa. This is found from Table A-5 on page 916.
Since the mass is constant
and the volume doubles, the final specific volume is twice the initial specific
volume: v3 = 2v2 = 1.43746 m3/kg. The final state with this specific volume and
a pressure of 300 kPa (0.3 MPa) is found in the superheat tables, Table A-6 on
page 918, to occur at a temperature between 600oC and 700oC. The final temperature is found by
interpolation.
`
So the final temperature, T3
= 662oC.
The initial internal
energy for the saturated vapor state is found from Table A-5, u1 = ug(250
kPa) = 2536.8 kJ/kg. The internal energy
at the final state is found by an interpolation similar to the one used for the
temperature.
The heat transfer is found
from the usual equation for the first law.
Q = m(u3 – u1)
+ W = (1.113 kg)(3412.3 – 2536.8)kJ/kg + 240 kJ = 1214 kJ.



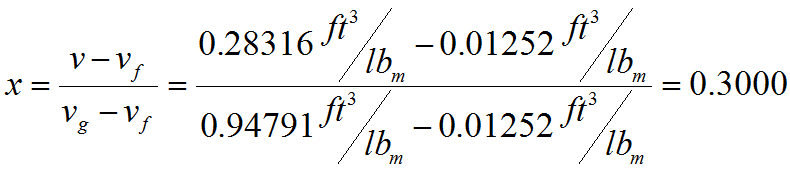











No comments:
Post a Comment